Superelevation & its Design Formula | Advantages | Highway Engineering

Superelevation or Banking of Road:-

When a vehicle travels in a circular path or curved path, it is subjected to an outward force which makes a vehicle to overturn and skid due to Centrifugal force. To overcome this force and for safe travel of a vehicle, the outer edge of the road is raised above the inner edge. This is known as superelevation or banking of road.

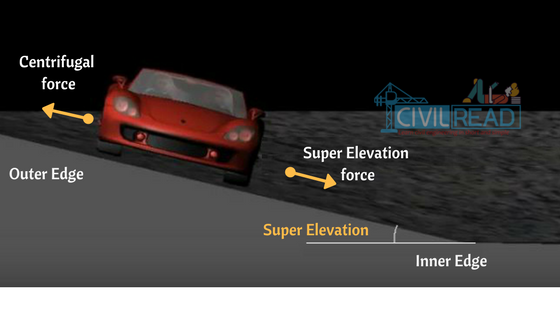
SuperElevation / Banking of road reduces the effect of centrifugal force on the running wheels. If superelevation is not provided with the entire centripetal force is produced by the friction between the vehicle’s tires and the roadway, thus results in reducing the speed of a vehicle.

Advantages of providing Super elevation:-

1. Super elevation is provided to achieve the higher speed of vehicles.
   It increases the stability of fast-moving vehicles when they pass through a horizontal curve, and it also decreases the stresses on the foundation.
2. In the absence of super elevation on the road along curves, potholes are likely to occur at the outer edge of the road.
3. The Indian road congress(IRC) has prescribed the max value of Super Elevation is 1 in 15.

Derivation of Super Elevation :

As per the figure, the below forces are acting on a car

In order to find out the angle of elevation (Super Elevation) the “tan” formula is used

From above fig,    tanθ  = ^{Opposite Side}⁄_{Adjacent Side}

therefore,               tanθ  = ^E⁄_B

The below forces are acting on the vehicle as mentioned in figure:

Weight of the vehicle     = W kg (↓) ; 

Centripetal force             = P (→);

Frictional forces              = F₁ & F₂ (← ); 

You can check out the below figure more idea.

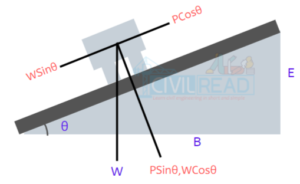
Hence, P.Cosθ  = W.Sinθ+F₁+F₂
where              F = fR

P.Cosθ = WSinθ + fR₁ + fR₂

= W.Sinθ + f(R₁ + R₂)

= W.Sinθ + f(PSinθ+WCosθ)

P.Cosθ-f.PSinθ = W.Sinθ+f.WCosθ

Divide with “W.Cosθ”;

^{(P.Cosθ-f.PSinθ)}⁄_W.Cosθ  = ^{(W.Sinθ+f.WCosθ)}⁄_W.Cosθ

             ^P⁄_W -(^f.P⁄_W)tanθ = tanθ + f

                 ^P⁄_W (1-f.tanθ) = tanθ+f

                                       ^P⁄_W = ^(tanθ+f)⁄_1-f.tanθ       

                                       ^P⁄_W = e + f

But, ^P⁄_W = V²/ gR

Therefore,            e + f = V²/ gR

Where,

e = rate of Super elevation in %

V = velocity of vehicle in m/s

f = lateral friction factor = 0.15

g = acceleration due to gravity = 9.81 m/s²

R = radius of circular curve in meters.

If velocity is in KMPH then  e + f = V²/ 127R

Super Elevation formula:-

The above formula is used only to calculate one of the missing value either e or f or V or R for design purpose consider the below procedure.

Design procedure of Superelevation / Banking of road:-

Design procedure includes following steps

Step – 1:-

Calculate the Super elevation (e) necessary for 75% design speed[0.75V] and assume no lateral friction is developed

As per practical conditions, it is suggested that superelevation should be provided to fully counteract the centrifugal force due to 75% of the Design Speed(V) by neglecting lateral friction (f=0) developed.

Super Elevation formula = e + f = [V²]/127R

Consider lateral friction f = 0;

75% of design speed which means V= 0.75V

As per formula,

e + f = [V²]/127R

e + 0 = [0.75V]²/127R

e = V² / 225R

Note: e value should not be more than 0.07 

If the calculated value (e_cal) is less than (e_max) then consider the value of (e_cal) if not proceed to next step,

if  (e_cal<e_max) then e = e_cal  

If the calculated value (e_cal) is greater than (e_max) then consider the value of (e_max)

if  (e_cal<e_max) then e = e_max  

Step – 2:-

Lets assume e = e_max   = 0.07 and proceed to next step.

Step-3: Calculate the value of friction for ‘e’ Value

Super Elevation formula = e + f = [V²]/127R

= 0.07 +f = [V²]/127R

f = [V²]/127R – 0.07

Step – 3:-

From the above step we found the value of e. Now lets find the value of the lateral friction (f) for the known value of e_max Value

Super Elevation = e_max + f = [V²]/127R

= 0.07 + f = [V²]/127R

f_cal   = [V²/127R] – 0.07 

If f_cal < f_max (0.15)

Then f_cal = f ;

If f_cal  > f_max (0.15)

Then e = 0.07 is safe.

But if f_cal > 0.15

Then f_cal =f_max (0.15)

Step – 4:-

Lets calculate the value of Restricted Speed (V_a)

Therefore V = V_a

Super Elevation = e + f = [V²]/127R

= 0.07 + 0.15 = (V_a)²/127R

V = [127R(0.22)]^1/2

If V_a > V then e = 0.07, f = 0.15

If V_a < V still e = 0.07 and f = 0.15 but the speed restriction board is provided along with consists the value of V_a

Segregation and Bleeding in concrete, Effects, Remedies 

How to calculate Quality of Fine aggregate /  Sand on site?

 LIKE US ON FACEBOOK

For Instant updates Join our Whatsapp Broadcast. Save our Whatsapp contact +9700078271 as Civilread and Send us a message “JOIN”

Never Miss an update Click on “Allow US” and make us allow or Click on Red notification bell at bottom right and allow notifications.
Stay tuned!